跳至主要內容

直线与圆锥曲线

Guitar大约 6 分钟数学

直线

直线方程

k：直线斜率。b：Y轴截距。α\alpha：倾斜角，和X轴的夹角。

k=tan⁡α,α=arctan⁡kk=\tan \alpha, \alpha = \arctan k。

斜截式：

y=kx+b y=kx+b

点斜式：

y−y0=k(x−x0)b=y0−kx0 y-y_0=k(x-x_0) \\\\ b=y_0-kx_0

两点式：

y−y0y1−y0=x−x0x1−x0k=y1−y0x1−x0 \frac{y-y_0}{y_1-y_0} = \frac{x-x_0}{x_1-x_0} \\\\ k = \frac{y_1-y_0}{x_1-x_0}

一般式：

Ax+By+C=0k=−ABb=−CB Ax+By+C=0 \\\\ k = -\frac AB \\ b=-\frac CB

两点式转一般式：

A=y1−y2B=x2−x1C=x1y2−x2y1=∣x1y1x2y2∣ \begin{aligned} A &= y_1 - y_2 \\\\ B &= x_2 - x_1 \\\\ C &= x_1y_2 - x_2y_1\\ &=\begin{vmatrix} x_1 & y_1 \\ x_2 & y_2 \end{vmatrix} \end{aligned}

点斜式转一般式：

y−y0=k(x−x0)kx−y+(y0−kx0)=0A=kB=−1C=y0−kx0 y-y_0=k(x-x_0) \\ kx - y + (y_0 - kx_0) = 0 \\\\ \begin{align} A &= k\\ B &= -1\\ C &= y_0 - kx_0 \end{align}

直线平行与垂直

平行 ⇔\Leftrightarrow 斜率相等。

A1A2+B1B2=0 A_1A_2+B_1B_2=0

垂直 ⇔\Leftrightarrow k1×k2=−1k_1 \times k_2=-1。

直线夹角

直线l1l_1、l2l_2。

θ1\theta_1：l1l_1 逆时针旋转到 l2l_2 所需的角度。

θ2\theta_2：l2l_2 逆时针旋转到 l1l_1 所需的角度。

有：θ1+θ2=π\theta_1+\theta_2=\pi。

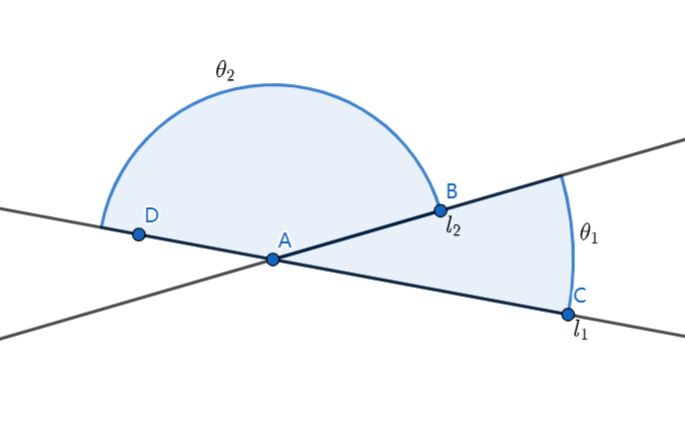
image-20230506141016214

记：两直线的夹角α=min⁡{θ1,θ2}\alpha = \min \{ \theta_1, \theta_2 \}。则α\alpha必为锐角。

有：

tan⁡α=∣k2−k11+k1k2∣tan⁡θ1=A1B2−A2B1A1A2+B1B2=∣A1B1A2B2∣[A2B2][A1B1] \tan \alpha = \left| \frac{k_2-k_1}{1+k_1k_2} \right| \\\\ \begin{align} \tan \theta_1 &= \frac {A_1B_2-A_2B_1}{A_1A_2+B_1B_2} \\\\ &= \frac { \begin{vmatrix} A_1 & B_1 \\ A_2 & B_2\end{vmatrix} } { \begin{bmatrix} A_2 & B_2 \end{bmatrix} \begin{bmatrix} A_1 \\B_1 \end{bmatrix} } \end{align}

点到直线的距离

水平距离：

dx=∣Ax0+By0+CA∣ d_x = \left| \frac{ Ax_0+By_0+C }{A} \right|

纵向距离：

dy=∣Ax0+By0+CB∣ d_y = \left| \frac{ Ax_0+By_0+C }{B} \right|

垂直距离：

d=∣Ax0+By0+C∣A2+B2=dxdydx2+dy2 \begin{align} d &= \frac { \left| Ax_0+By_0+C \right| }{ \sqrt{A^2+B^2} } \\\\&= \frac {d_xd_y}{\sqrt{d_x^2+d_y^2}} \end{align}

垂足坐标：

x′=B2x0−ABy0−ACA2+B2y′=A2y0−ABx0−BCA2+B2 \begin{aligned} x' &= \frac{B^2x_0 - ABy_0 - AC}{A^2 + B^2} \\ y' &= \frac{A^2y_0 - ABx_0 - BC}{A^2 + B^2} \end{aligned}

圆

圆的方程

标准方程：

(x−a)2+(y−b)2=r2 (x-a)^2+(y-b)^2=r^2

圆心：(a,b)(a,b)，半径：rr。

一般方程：（二元二次方程）

Ax2+Bxy+Cy2+Dx+Ey+F=0x2+y2+Dx+Ey+F=0→(x+D2)2+(y+E2)2=D2+E2−4F4=Δ Ax^2+Bxy+Cy^2+Dx+Ey+F=0 \\ \\x^2+y^2+Dx+Ey+F=0 \\\to(x+\frac D2)^2+(y+\frac E2)^2=\frac {D^2+E^2-4F}4 = \Delta

有：Δ>0\Delta>0，圆；Δ=0\Delta=0，一个点；Δ<0\Delta<0，无图形。根据三个点求出D、E、F即可确定唯一圆。

正圆：(0,0)(0,0)。

x2+y2=r2 x^2+y^2=r^2

偏心圆：(a,0),(0,b)(a,0),(0,b)。

(x−a)2+y2=r2→x2+y2=r2−a2+2axx2+(y−b)2=r2→x2+y2=r2−b2+2by (x-a)^2+y^2=r^2 \\\to x^2+y^2=r^2-a^2+2ax \\\\ x^2+(y-b)^2=r^2 \\\to x^2+y^2=r^2-b^2+2by

圆的几何意义

  1. 到定点 (a,b)(a,b) 的定长 rr 的点的集合。(x−a)2+(y−b)2=r2(x-a)^2+(y-b)^2=r^2
  2. 到两定点 (x1,y1),(x2,y2)(x_1,y_1),(x_2,y_2) 距离定比 ee 的点的集合。

(x−x1)2+(y−y1)2(x−x2)2+(y−y2)2=e(x−x1)2+(y−y1)2=e2[(x−x2)2+(y−y2)2]→(1−e2)∗x2+(1−e2)∗y2+2∗(e2∗x2−x1)∗x+2∗(e2∗y2−y1)∗y=e2∗(x22+y22)−(x12+y12) \frac {\sqrt{(x-x_1)^2+(y-y_1)^2}}{\sqrt{(x-x_2)^2+(y-y_2)^2}}=e \\\\ (x-x_1)^2+(y-y_1)^2=e^2[(x-x_2)^2+(y-y_2)^2] \\\to (1 - e^2)*x^2+ (1 - e^2)*y^2 + 2*(e^2 * x_{2} - x_{1})*x + 2*(e^2 * y_{2} - y_{1})*y = e^2 * (x_{2}^2 + y_{2}^2) - (x_{1}^2 + y_{1}^2)

渐开线

圆上一点绕圆不断延长转轴的旋转轨迹。

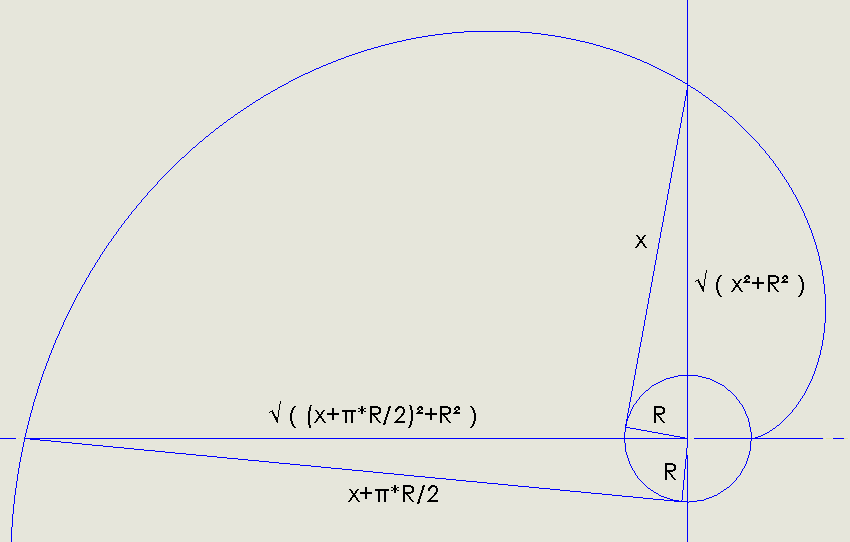
解渐开线方程_百度知道

圆：x2+y2=r2x^2+y^2=r^2。

渐开线方程：

{x=r(cos⁡ψ+ψsin⁡ψ)y=r(sin⁡ψ−ψcos⁡ψ) \begin{cases} x=r(\cos \psi+\psi \sin \psi)\\ y=r(\sin \psi - \psi \cos \psi) \end{cases}

摆线

圆上一点随圆滚动的轨迹。

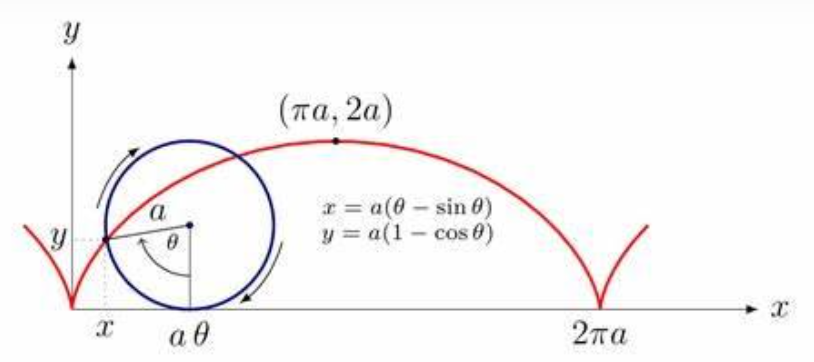
image-20230506164847531

圆：x2+y2=a2x^2+y^2=a^2。

θ\theta：圆累计滚动的角度。

摆线方程：

{x=a(θ−sin⁡θ)x=a(1−cos⁡θ) \begin{cases} x=a(\theta-\sin \theta)\\ x=a(1-\cos \theta) \end{cases}

椭圆

焦点：F1,F2F_1,F_2。

焦距：两焦点之间的距离，2c2c。

中心：椭圆的对称中心。

顶点：椭圆与两条对称轴的四个交点。

长轴：焦点所在轴的两个顶点围成的线段，长 2a2a。

短轴：与长轴相对，长 2b2b。

离心率：焦距与长轴 的长之比，e=cae=\frac ca。

准线：垂直于长轴，绝对值为 ee 的直线。在椭圆外侧的直线。

  • 焦点在x轴，则为 l:x=±el:x=\pm e
  • 焦点在y轴，则为 l:y=±el:y=\pm e

有：

  • c2=a2−b2c^2=a^2-b^2。
  • a>b>0a>b>0。
  • 0<e<10<e<1。
  • ee 越接近0，越圆；越接近1，越扁。

椭圆方程

标准方程：

  • 焦点在x轴上，F：(−c,0),(c,0)(-c,0),(c,0)

x2a2+y2b2=1 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1

  • 焦点在y轴上，F：(0,−c),(0,c)(0,-c),(0,c)

y2a2+x2b2=1 \frac{y^2}{a^2}+\frac{x^2}{b^2}=1

椭圆的几何意义

  1. 到两定点（焦点F）距离定和 2a2a 的点的集合。
  2. 到一定点（焦点）和一定直线（准线）的距离定比 e(e<1)e(e<1) 的点的集合。（焦点和准线处于同半轴）

椭圆切线

椭圆：x2a2+y2b2=1\frac{x^2}{a^2}+\frac{y^2}{b^2}=1。

切线方程；

x0⋅xa2+y0⋅yb2=1 \frac{x_0\cdot x}{a^2}+\frac{y_0\cdot y}{b^2}=1

双曲线

焦点：F1,F2F_1,F_2。

焦距：两焦点之间的距离，2c2c。

中心：双曲线的对称中心。

实轴：焦点所在的轴，长 2a2a。

虚轴：与实轴相对，长 2b2b。

顶点：双曲线与实轴的两个交点，(±a,0)(\pm a,0)或(0,±a)(0,\pm a)。

虚顶点：虚轴的两个点，(0,±b)(0,\pm b)或(±b,0)(\pm b,0)。

内矩形：顶点和虚顶点可以确定一个四边平行坐标轴的矩形。

渐近线：过内矩形对角线的两条直线。

  • 焦点在x轴：y=baxy=\frac bax。
  • ？焦点在y轴：y=abxy=\frac abx。

离心率：焦距与实轴长之比，e=cae=\frac ca。

准线：垂直于实轴，在双曲线内侧的直线。

  • 焦点在x轴，则为 l:x=±a2cl:x=\pm \frac{a^2}c。
  • 焦点在y轴，则为 l:y=±a2cl:y=\pm \frac{a^2}c 。

有：

  • c2−a2=b2c^2-a^2=b^2。
  • c>a>0c>a>0，c>b>0c>b>0。
  • ba=e2−1\frac ba=\sqrt{e^2-1}。（渐近线斜率）
  • ee 越大，双曲线开口越大，渐近线越陡峭；越小，开口越小，渐近线越平稳。

双曲线方程

标准方程：

  • 焦点在x轴上，F：(−c,0),(c,0)(-c,0),(c,0)

x2a2−y2b2=1∣x2y2a2b2∣=a2b2 \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \\\\ \begin{vmatrix} x^2 & y^2\\ a^2 & b^2 \end{vmatrix}=a^2b^2

  • 焦点在y轴上，F：(0,−c),(0,c)(0,-c),(0,c)

y2a2−x2b2=1∣y2x2a2b2∣=a2b2 \frac{y^2}{a^2}-\frac{x^2}{b^2}=1 \\\\ \begin{vmatrix} y^2 & x^2\\ a^2 & b^2 \end{vmatrix}=a^2b^2

双曲线的几何意义

  1. 到两定点（焦点F）距离定差 2a2a 的点的集合。
  2. 到一定点（焦点）和一定直线（准线）的距离定比 e(e>1)e(e>1) 的点的集合。（焦点和准线处于同半轴）

双曲线切线

双曲线：x2a2−y2b2=1\frac{x^2}{a^2}-\frac{y^2}{b^2}=1。

切线方程：

x0⋅xa2−y0⋅yb2=1 \frac{x_0\cdot x}{a^2}-\frac{y_0\cdot y}{b^2}=1

抛物线

焦点：FF。

准线：垂直于FF所在轴，且不与FF在同半轴的一条直线。只有一条准线。

  • 焦点在x轴，则为 l:x=∓p2l:x=\mp \frac p2。（其一）
  • 焦点在y轴，则为 l:y=∓p2l:y=\mp \frac p2 。（其一）

轴：抛物线的对称轴。

顶点：抛物线和轴的交点。

离心率：抛物线上一点到F的距离和到准线的距离之比，定义上，e≡1e \equiv 1。

  • 抛物线没有渐近线。

通径：垂直于轴，交抛物线于两点，所连成的线段，长 2p2p。

抛物线方程

标准方程：

  • 焦点在x轴，F：(p2,0)(\frac p2,0)或(−p2,0)(-\frac p2,0)。

y2=2pxF(p2,0)y2=−2pxF(−p2,0) y^2=2px F(\frac p2,0)\\ y^2=-2px F(-\frac p2,0)

  • 焦点在y轴，F：(0,p2)(0,\frac p2)或(0,−p2)(0,-\frac p2)。

x2=2pyF(0,p2)x2=−2pyF(0,−p2) x^2=2py F(0,\frac p2)\\ x^2=-2py F(0,-\frac p2)

焦点所在的半轴是抛物线的开口方向，如果是负半轴，则需要加负号。

抛物线的几何意义

到一定点（焦点）和一定直线（准线）的距离定比 e(e=1)e(e=1) 的点的集合。

抛物线切线、法线

对于抛物线：y2=2pxy^2=2px。

切线方程：

y−y0=py0(x−x0)y02=2px0→y⋅y0=p(x+x0) y-y_0=\frac p{y_0}(x-x_0) \\y_0^2=2px_0 \\\to y\cdot y_0=p(x+x_0)

法线方程：

y−y0=−y0p(x−x0) y-y_0=-\frac {y_0}p(x-x_0)

Copyright ©2024-present Guitar